个人信息Personal Information
出生日期：1987-05-29
入职时间：2015-08-28
学历：博士研究生毕业
办公地点：交大犀浦校区第三号教学楼30439室
性别：男
在职信息：在岗
主要任职：数学学院院长助理
其他任职：Supervisor of graduate students
毕业院校：新加坡国立大学
学科：数学. 统计学
所在单位：数学学院
报考该导师研究生的方式
欢迎你报考黄磊老师的研究生，报考有以下方式：
1、参加西南交通大学暑期夏令营活动，提交导师意向时，选择黄磊老师，你的所有申请信息将发送给黄磊老师，老师看到后将和你取得联系，点击此处参加夏令营活动
2、如果你能获得所在学校的推免生资格，欢迎通过推免方式申请黄磊老师研究生，可以通过系统的推免生预报名系统提交申请，并选择意向导师为黄磊老师，老师看到信息后将和你取得联系，点击此处推免生预报名
3、参加全国硕士研究生统一招生考试报考黄磊老师招收的专业和方向，进入复试后提交导师意向时选择黄磊老师。
4、如果你有兴趣攻读黄磊老师博士研究生，可以通过申请考核或者统一招考等方式报考该导师博士研究生。
数据会聊天之用Python实现GARCH建模
## 今天展示的主要内容是用Python做GARCH模型的模拟实验和真实数据分析，真实数据源自标准普尔500指数，模型拟合和预测结果都将呈现。另外，还会介绍一个从雅虎网站爬取股票数据的工具，以及一个常用的时间序列画图函数。
import datetime as dt #时间格式，用于网上爬股票数据
from arch.univariate import arch_model # 进行一元ARCH或GARCH模型建模的函数
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.tsa.api as smt
import pandas_datareader.data as web # 网络爬数据程序包
import matplotlib.pyplot as plt
## 构造一个画图函数
def tsplot(y, lags=None, figsize=(10, 8), style='bmh'):
if not isinstance(y, pd.Series): #判断类型
y = pd.Series(y)
with plt.style.context(style):
layout = (3, 2)
ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1, 0))
pacf_ax = plt.subplot2grid(layout, (1, 1))
qq_ax = plt.subplot2grid(layout, (2,0))
y.plot(ax=ts_ax)
ts_ax.set_title('Time Series Analysis Plots')
smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5)
smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5)
sm.qqplot(y, line='s', ax=qq_ax)
qq_ax.set_title('QQ Plot')
plt.tight_layout()
return
##简单ARCH(1)模拟
np.random.seed(23) #随机种子
a0 = 2.24
a1 = 0.6 # ARCH模型的设定参数
y = w = np.random.normal(size=500) #正态分布随机数
Y = np.empty_like(y)
for t in range(len(y)):
Y[t] = w[t] * np.sqrt((a0 + a1*y[t-1]**2))
# Y[t]即为满足ARCH(1)模型的模拟序列
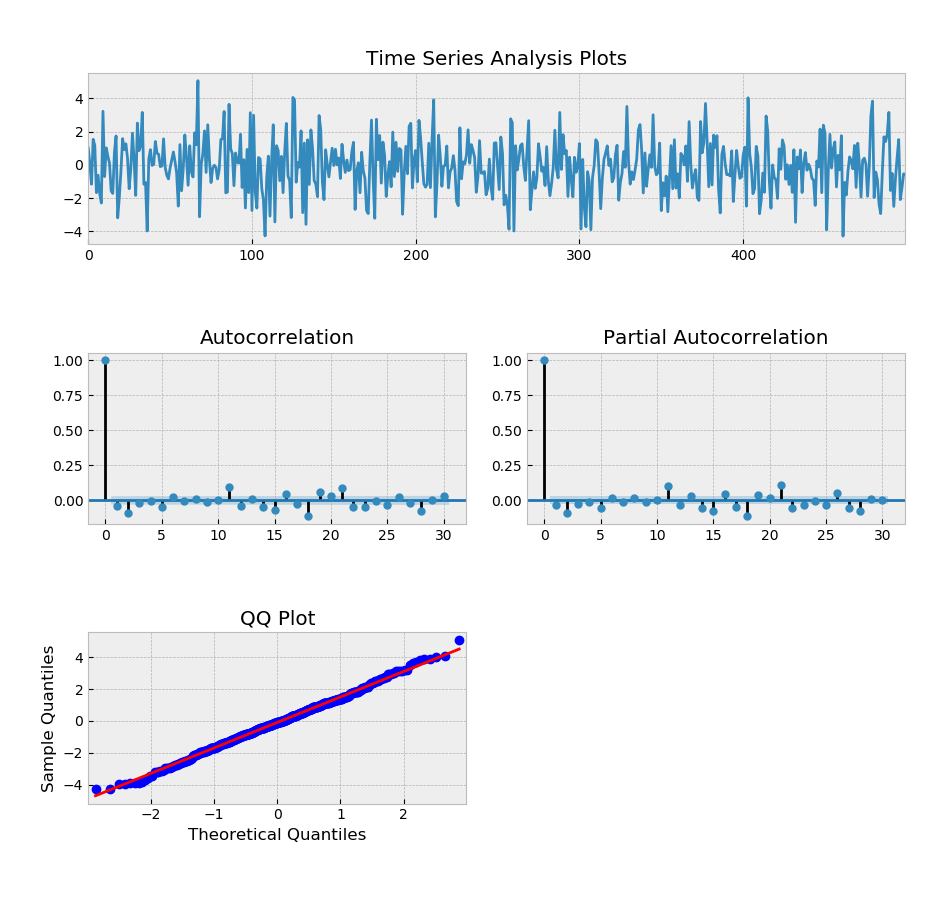
tsplot(Y, lags=30)# 考察原序列的自相关图
plt.figure()
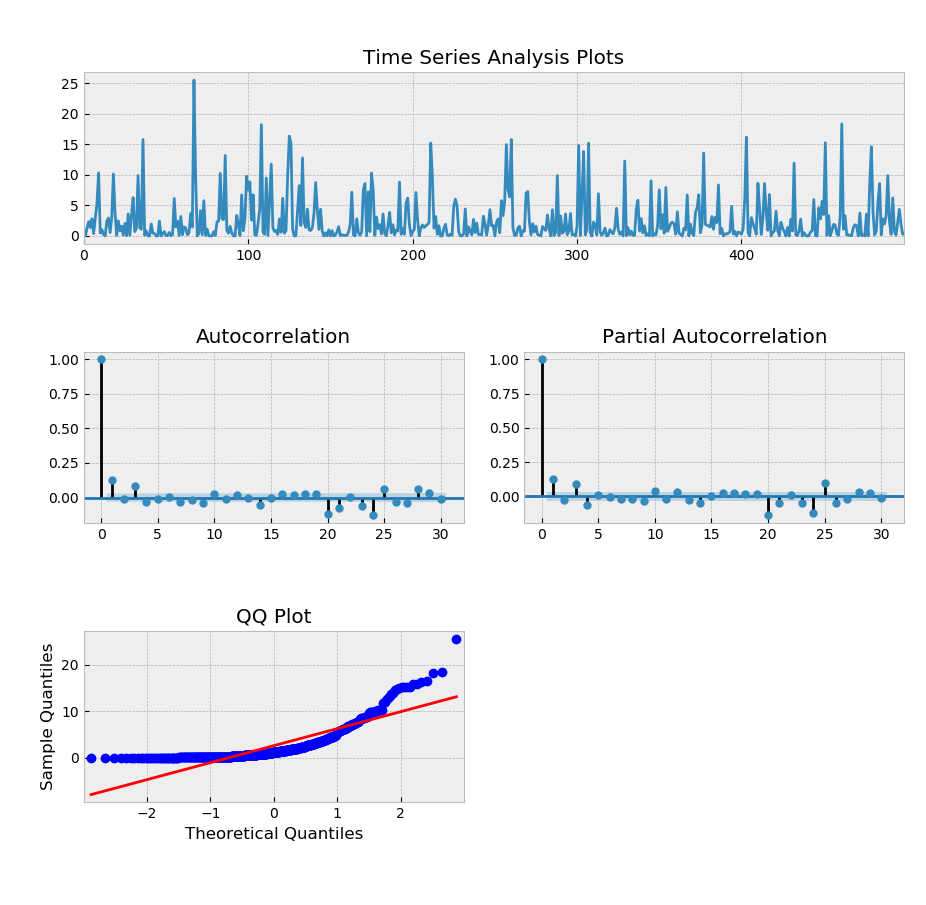
tsplot(Y**2, lags=30) #考察原序列平方的自相关图
plt.figure()
## GARCH(1,1)模拟
np.random.seed(2)
a0 = 0.2
a1 = 0.5
b1 = 0.3
n = 10000
w = np.random.normal(size=n)
eps = np.zeros_like(w)
sigsq = np.zeros_like(w)
for i in range(1, n):
sigsq[i] = a0 + a1*(eps[i-1]**2) + b1*sigsq[i-1]
eps[i] = w[i] * np.sqrt(sigsq[i])
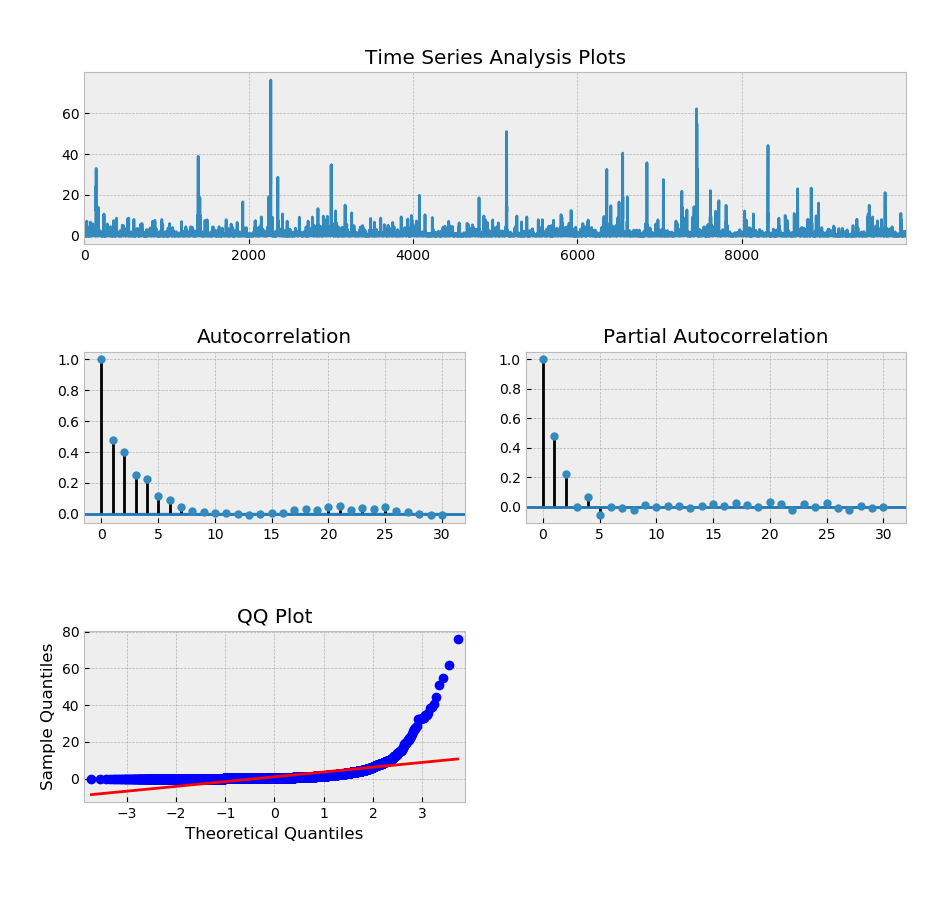
# eps即满足GARCH(1,1)模型的模拟序列
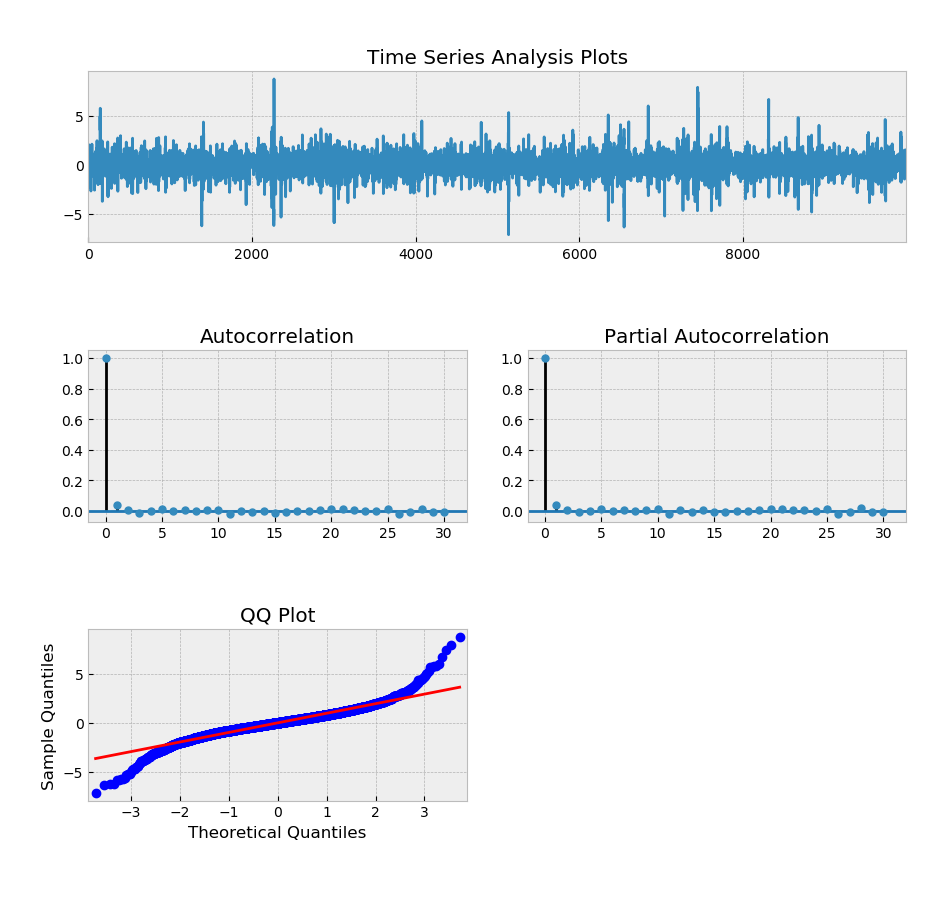
tsplot(eps, lags=30) #考察序列自相关图
plt.figure()
tsplot(eps**2, lags=30) #考察序列平方的自相关图
plt.figure()
# 做参数估计
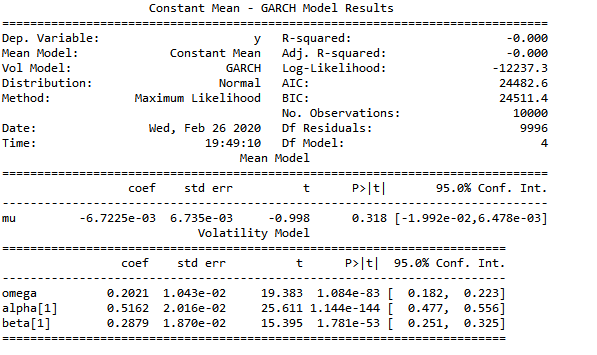
am = arch_model(eps) #若不作任何参数设定，则默认为GARCH(1,1)模型
res = am.fit() #拟合结果，参数估计和模拟设定值很接近
print(res.summary())
##标准普尔500指数实例分析
start = dt.datetime(2015,1,1) # 爬数据起始时间
end = dt.datetime(2020,1,1) #爬数据结束时间，五年时间
sp500 = web.get_data_yahoo('SPY', start=start, end=end) # Yahoo网上，SPY即Standard&Poor500指数的缩写
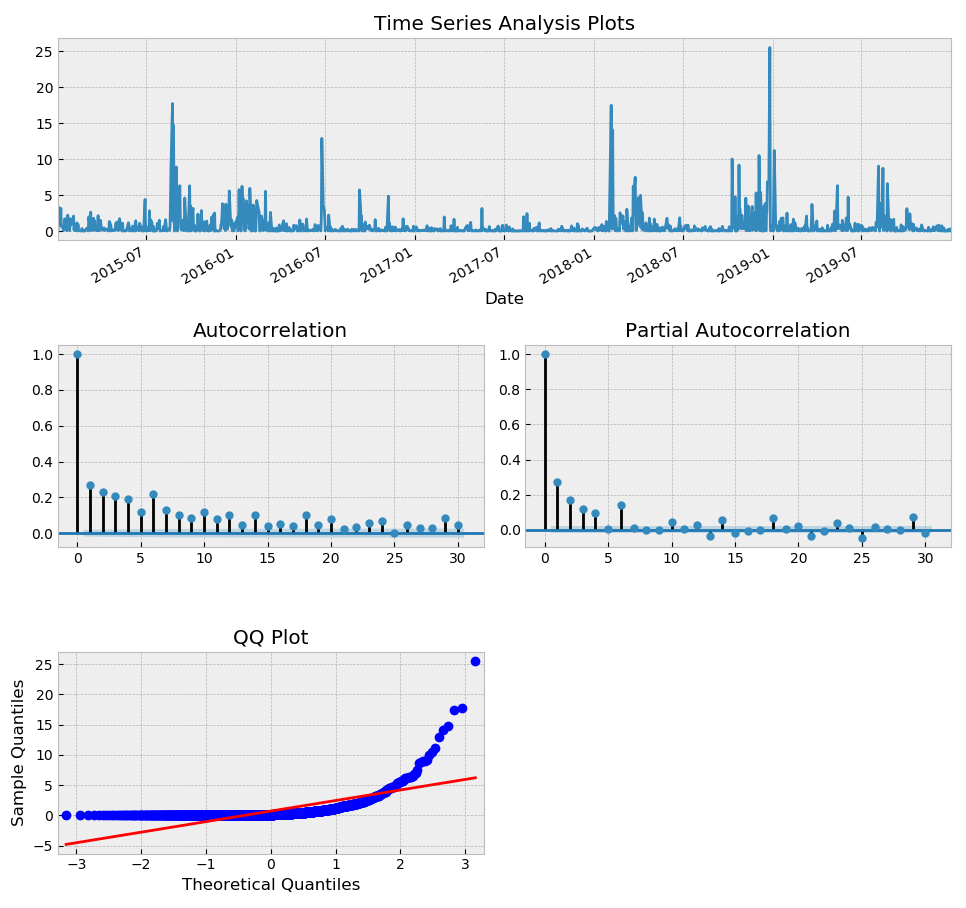
returns = 100 * sp500['Close'].pct_change().dropna() # 价格转换成收益率
tsplot(returns**2,lags=30) #收益率平方有明显的群聚效应，适合建立GARCH模型
plt.figure()
returns.shape
#对SPY收益率拟合GARCH(1,1)模型
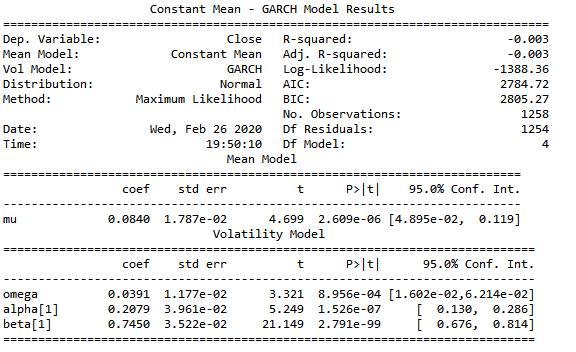
model=arch_model(returns, vol='Garch', p=1, o=0, q=1, dist='Normal')
results=model.fit()
print(results.summary()) #模型参数皆显著
#对未来收益率用模拟预测
forecasts = results.forecast(horizon=30, method='simulation', simulations=500) #模拟500次
sims = forecasts.simulations
sims.values.shape # 对每一个t时刻的return, 往后预测steps=30, 模拟500次
lines = plt.plot(sims.values[-1,:,:].T, color='blue',alpha=0.05)# 模拟结果作图
plt.figure()
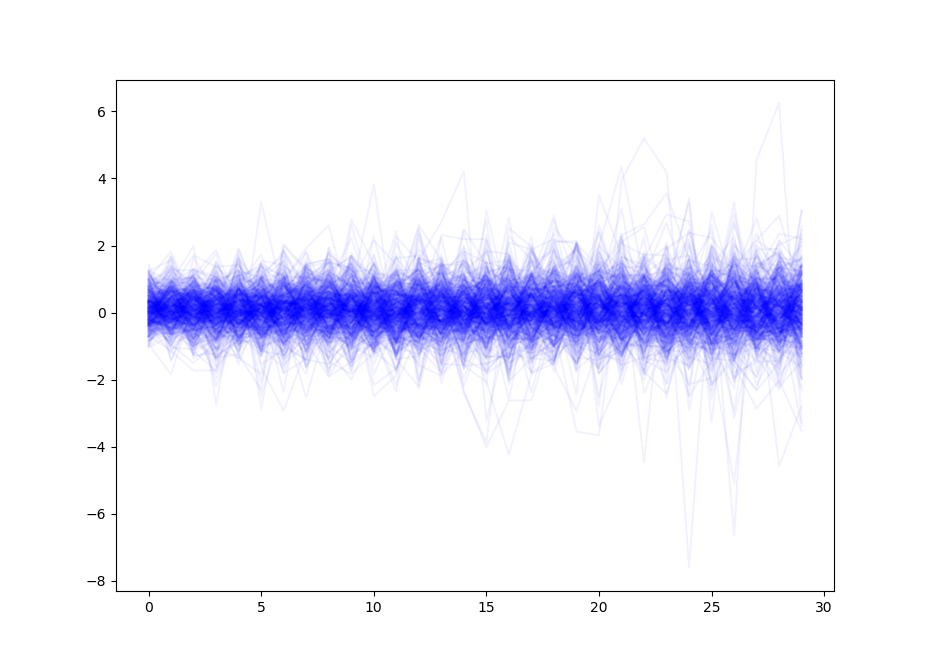
#1步预报和30步预报对比图
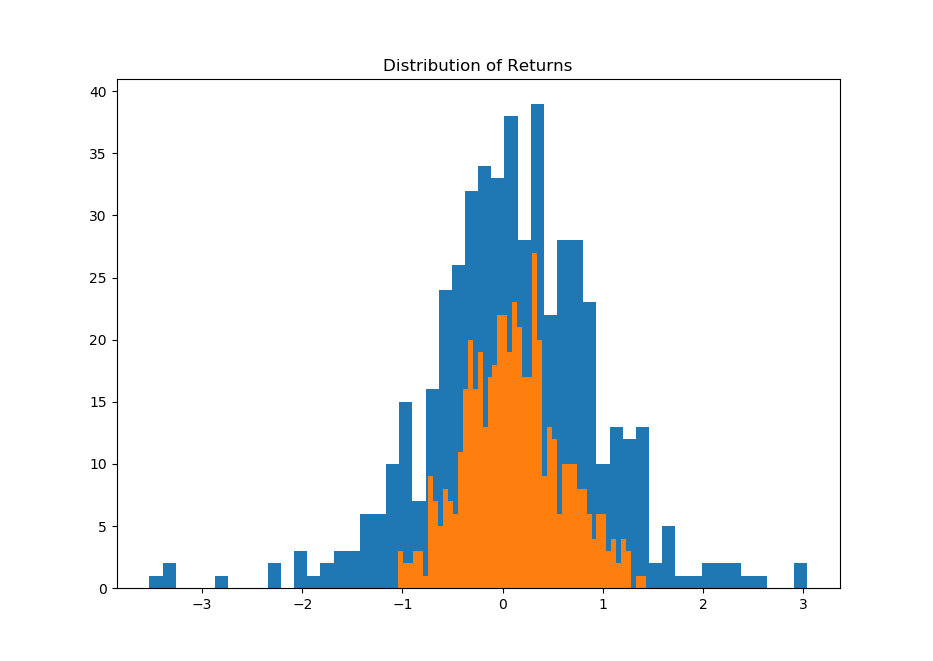
plt.hist(sims.values[-1,:,-1],bins=50)
print(np.percentile(sims.values[-1,:,-1].T,5))
plt.hist(sims.values[-1, :,0],bins=50)
print(np.percentile(sims.values[-1,:,0].T,5))
plt.title('Distribution of Returns') # 橙色的是1步预报(500次模拟直方图)，蓝色的是30步预报，明显步长越大方差越大
