个人信息Personal Information
出生日期：1987-05-29
入职时间：2015-08-28
学历：博士研究生毕业
办公地点：交大犀浦校区第三号教学楼30439室
性别：男
在职信息：在岗
主要任职：数学学院院长助理
其他任职：Supervisor of graduate students
毕业院校：新加坡国立大学
学科：数学. 统计学
所在单位：数学学院
报考该导师研究生的方式
欢迎你报考黄磊老师的研究生，报考有以下方式：
1、参加西南交通大学暑期夏令营活动，提交导师意向时，选择黄磊老师，你的所有申请信息将发送给黄磊老师，老师看到后将和你取得联系，点击此处参加夏令营活动
2、如果你能获得所在学校的推免生资格，欢迎通过推免方式申请黄磊老师研究生，可以通过系统的推免生预报名系统提交申请，并选择意向导师为黄磊老师，老师看到信息后将和你取得联系，点击此处推免生预报名
3、参加全国硕士研究生统一招生考试报考黄磊老师招收的专业和方向，进入复试后提交导师意向时选择黄磊老师。
4、如果你有兴趣攻读黄磊老师博士研究生，可以通过申请考核或者统一招考等方式报考该导师博士研究生。
数据会聊天之用Python预测时间序列
## 今天以一个叫Federal Reserve Board Production Index的数据为例，来展示如何用Python进行时间序列建模和预测，数据可从附件下载。使用的模型是Seasonal ARIMA。关于波动率的GARCH模型以后再分享。
##载入程序包, 第一期已经介绍了以下程序包，这里不再赘述
import pandas as pd
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
##读取数据
df=pd.read_csv("D:/mypy/Prod.csv") #我存在自己D盘mypy文件夹里，数据见附件
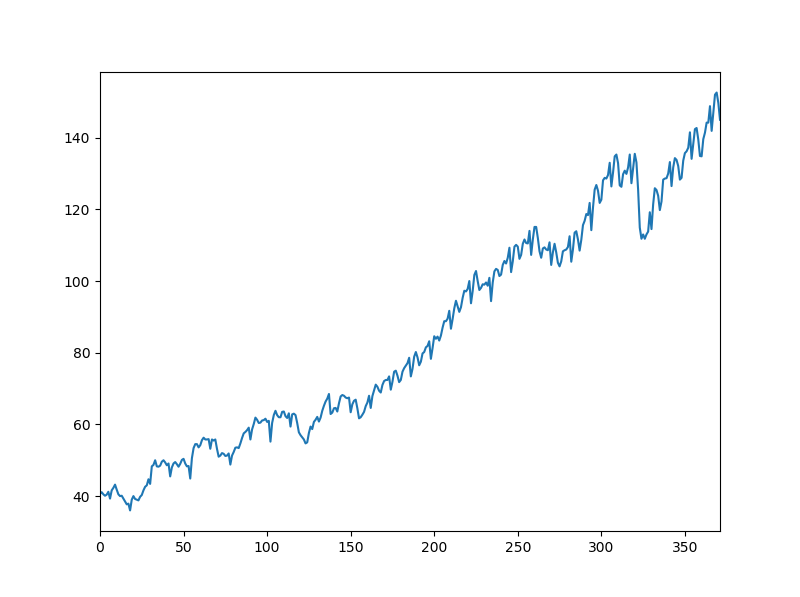
prod=df['x']
prod.plot(figsize=(8,6)) #设置图形大小
plt.show()
##相关性分析
data=pd.Series(prod) #转换成时序型数据
fig=plt.figure(figsize=(8,6)) #创建新图形窗口，并设置大小
ax1=fig.add_subplot(211) # 一个图形窗口设置成2行1列，在1行画图"ax1", 第二行画"ax2"
fig=sm.graphics.tsa.plot_acf(prod,lags=30,ax=ax1) #画自相关系数图ACF
ax2=fig.add_subplot(212)
fig=sm.graphics.tsa.plot_pacf(prod,lags=30,ax=ax2) #画偏相关系数图PACF
plt.show()
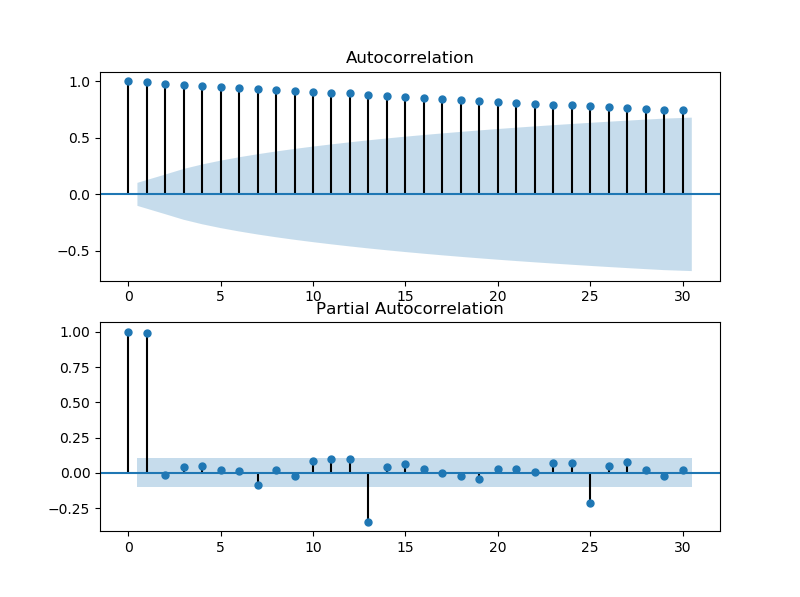
##有明显趋势，一阶差分
d1dat=np.diff(prod)
fig=plt.figure(figsize=(8,6)) #创建图形窗口，可设置大小
ax1=fig.add_subplot(211) # 一个图形窗口设置成2行1列，在1行画图"ax1", 第二行画"ax2"
fig=sm.graphics.tsa.plot_acf(d1dat,lags=30,ax=ax1) # 非常明显的年周期性, period=12
ax2=fig.add_subplot(212)
fig=sm.graphics.tsa.plot_pacf(d1dat,lags=30,ax=ax2)
plt.show()
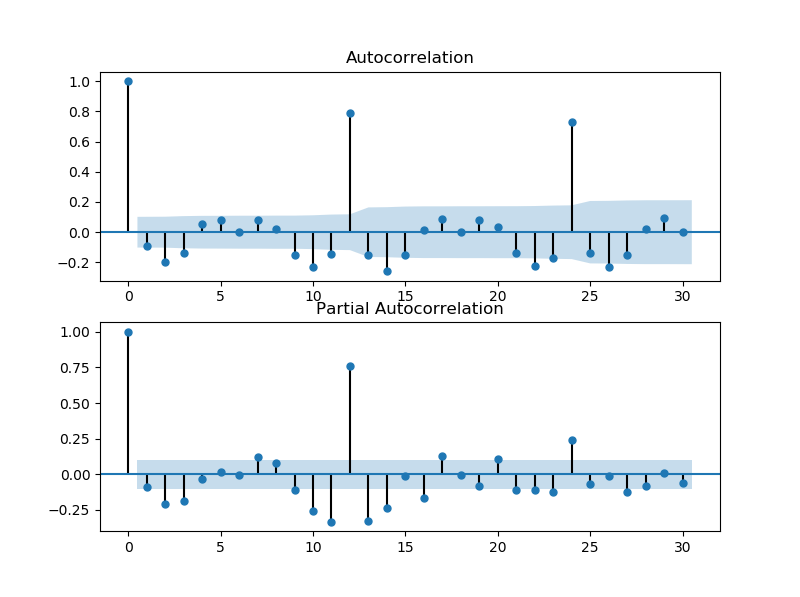
##模型拟合, 我们这里尝试一个ARIMA(p=1,d=1,q=1)*(P=2,D=1,Q=1)s=12的季节ARIMA模型
Sarima_mod=sm.tsa.SARIMAX(prod,order=(1,1,1),seasonal_order=(2,1,1,12)).fit() #模型拟合
Sarima_mod.summary() #拟合结果
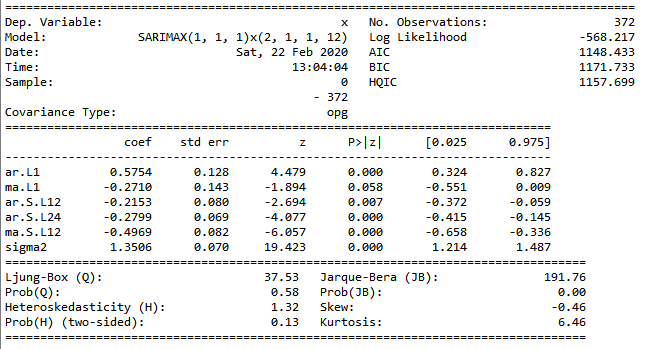
pred=Sarima_mod.get_forecast(steps=12) # 向后12步预测
pred.predicted_mean # 预测均值
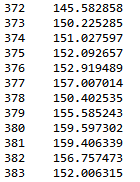
pred_ci=pred.conf_int() #预测置信区间
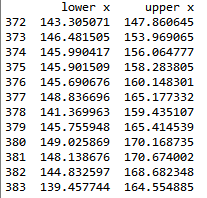
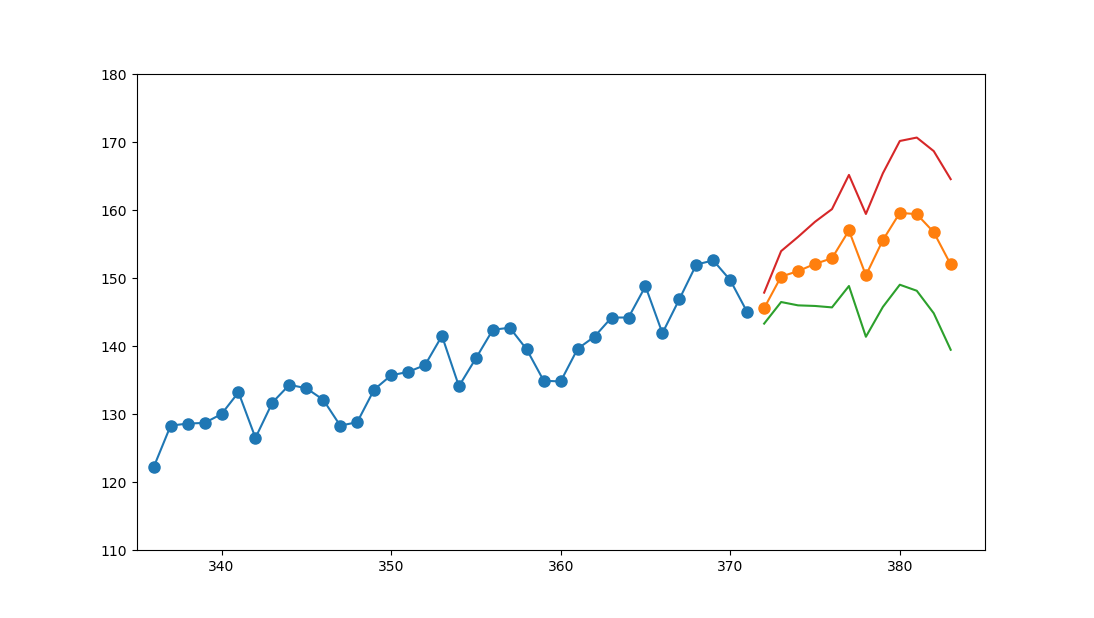
prodtc=prod[336:] #截断时序，为了方便看出预测趋势
fig=plt.figure()
prodtc.plot(figsize=(8,6)) #截断时序图
pred.predicted_mean.plot() # 12步预测均值
pred_ci['lower x'].plot() # 12步预测置信下限
pred_ci['upper x'].plot() #12步预测置信上限
plt.ylim((110,180))
plt.xlim((335,385)) #调整图像纵轴横轴范围，下图蓝色是原始截断时序，橙色是预测值，绿色红色是95%置信区间
