个人信息Personal Information
出生日期：1987-05-29
入职时间：2015-08-28
学历：博士研究生毕业
办公地点：交大犀浦校区第三号教学楼30439室
性别：男
在职信息：在岗
主要任职：数学学院院长助理
其他任职：Supervisor of graduate students
毕业院校：新加坡国立大学
学科：数学. 统计学
所在单位：数学学院
报考该导师研究生的方式
欢迎你报考黄磊老师的研究生，报考有以下方式：
1、参加西南交通大学暑期夏令营活动，提交导师意向时，选择黄磊老师，你的所有申请信息将发送给黄磊老师，老师看到后将和你取得联系，点击此处参加夏令营活动
2、如果你能获得所在学校的推免生资格，欢迎通过推免方式申请黄磊老师研究生，可以通过系统的推免生预报名系统提交申请，并选择意向导师为黄磊老师，老师看到信息后将和你取得联系，点击此处推免生预报名
3、参加全国硕士研究生统一招生考试报考黄磊老师招收的专业和方向，进入复试后提交导师意向时选择黄磊老师。
4、如果你有兴趣攻读黄磊老师博士研究生，可以通过申请考核或者统一招考等方式报考该导师博士研究生。
数据会聊天之用Python实现逻辑回归
## 本期是基于binary.csv数据来展示Python如何进行逻辑回归建模、预测和评估的工作。
## 载入所需程序包
from sklearn.model_selection import train_test_split # sklearn是一个机器学习程序包，这里使用它里面一个训练集和测试集分割函数
import pandas as pd #数据分析工具包
import statsmodels.api as sm #常用的统计学模型程序包
import pylab as pl #交互作图程序包
import numpy as np #数组与矩阵运算包
import seaborn as sbn #数据可视化包
from sklearn import metrics # metrics可以计算各种模型评估度量，如ROC曲线，AUC, R2，MSE, MAE，精确度等
## 读取数据
df=pd.read_csv("D:/mypy/binary.csv") #我存在自己D盘mypy文件夹里，数据从附件解压
df.head #观看部分数据结构
df.columns=["admit","gre","gpa","prestige"] #对变量命名，Y=admit 是否录取；X1=gre; X2=gpa; X3=prestige 为模型解释变量
## 初等统计量
df.describe() #描述统计， 均值，标准差，分位数，输出结果见下图
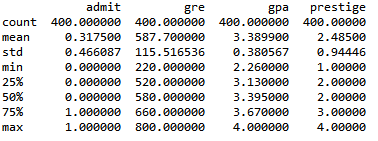
df.std() # 标准差
df.mean() #均值
pd.crosstab(df['admit'], df['prestige'], rownames=['admit']) #是否录取与毕业学校声望的列联表
df.hist() # 直方图，如下
pl.show()
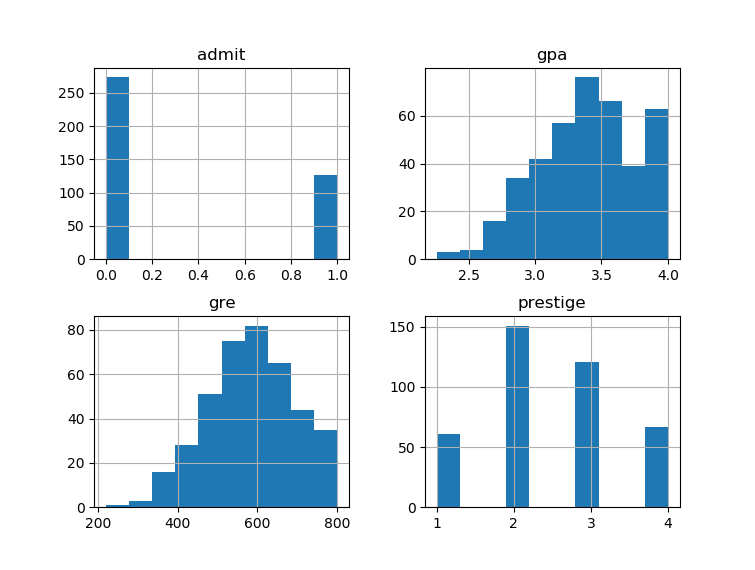
##构造哑变量
dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige') #把多分类变量prestige变成哑变量
dummy_ranks.head() #看看哑变量结构
cols_to_keep = ['admit', 'gre', 'gpa'] #响应变量+另外两个数值型变量
data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':]) # 新设计矩阵包含gre+gpa以及三个哑变量（四分类变量只能用三个哑变量）
data.head()#看看结构
data['intercept']=1#为设计矩阵添加元素为1的列向量，用来估计截距项，放在最后一列
##全样本拟合模型
train_cols=data.columns[1:] # python 中0代表第一个数，因此"[1:]"表示第二列及以后
logit=sm.Logit(data["admit"],data[train_cols]) #响应变量Y在前面，设计矩阵X在后
result=logit.fit() #调取拟合结果
result.summary()#查看拟合结果
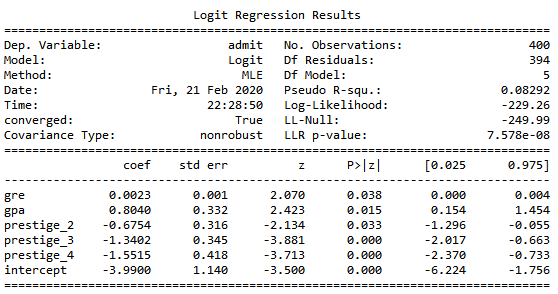
result.conf_int() # 参数的区间估计
np.exp(result.params) # 计算exp(β)
##训练和测试
X=data[train_cols]
y=data['admit']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=23) #将原数据集分为占比0.8的训练集和0.2的测试集
logit=sm.Logit(y_train,X_train)#训练集上拟合模型
result=logit.fit() # 调取拟合结果
y_p=result.predict(X_test) # 测试集上预测，这里y_p就是概率P(Y=1|X)
y_pre=(y_p>0.5) # 用阈值0.5来分类，这里python返回True or False的逻辑值
y_pred=np.array(y_pre,int) #逻辑值转换为整数值
##分类精度及热力图
confusion_mat=pd.crosstab(y_test, y_pred, rownames=['Actual'],colnames=['Prediction'])#真实值和预测值列联表，也称混淆矩阵
confusion_mat #展示结果
pl.figure()#创建新的图形窗口
sbn.heatmap(confusion_mat,annot=True)#画热力图，如下
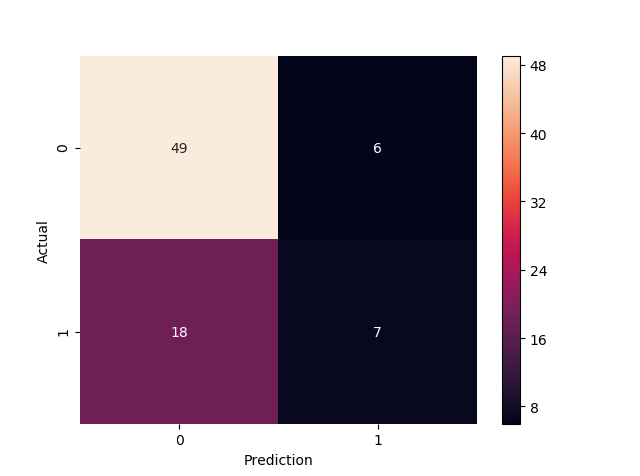
print('Accuracy:', metrics.accuracy_score(y_test, y_pred))# 准确度计算
##这里准确度计算值为0.7，并不高，比瞎猜强一些。你也可以调整测试集占比test_size，或者调整随机数种子random_state，看看不同结果。当然，我们是知道的，逻辑回归更注重解释力，预测能力不是它的强项，后期我们会介绍一个比逻辑回归预测能力强的常用机器学习方法。